Commercial math deals with all those concepts that people use in their everyday life. The word commercial itself means the economical world or something relating to buying or selling. It involves the concept of profit and loss, discounts, marked price, simple and compound interest, taxes, ratio and proportion, percentages, and everything that revolved around money. Let's learn about commercial math and all its sub-branches in math in detail in this lesson.
| 1. | Introduction to Commercial Math |
| 2. | Money |
| 3. | Ratio |
| 4. | Proportion |
| 5. | Unitary Method |
| 6. | Profit and Loss |
| 7. | Simple Interest |
| 8. | Compound Interest |
| 9. | Discounts |
| 10. | Taxes |
| 11. | FAQs on Commercial Math |
Commercial math focuses on those aspects of mathematics that are used in everyday life. Consider an example ; Eva, your friend goes to a stationary shop to buy a notebook. The shopkeeper tells her that 12 notebooks will cost $200. She has to calculate the cost of 1 notebook. This requires an understanding of the unitary method. Let’s take another example; Ron goes to buy a cricket bat with his mother. One shop offers him a 25% discount on the bat. The other shop offers a free cricket ball with the bat. Ron wants to help his mother select the best deal. He should know how to calculate percentages and also understand the concept of discounts.
In both these examples, we make use of commercial math concepts. You can go ahead and explore all important topics in Commercial Math by selecting the topics from this list below:
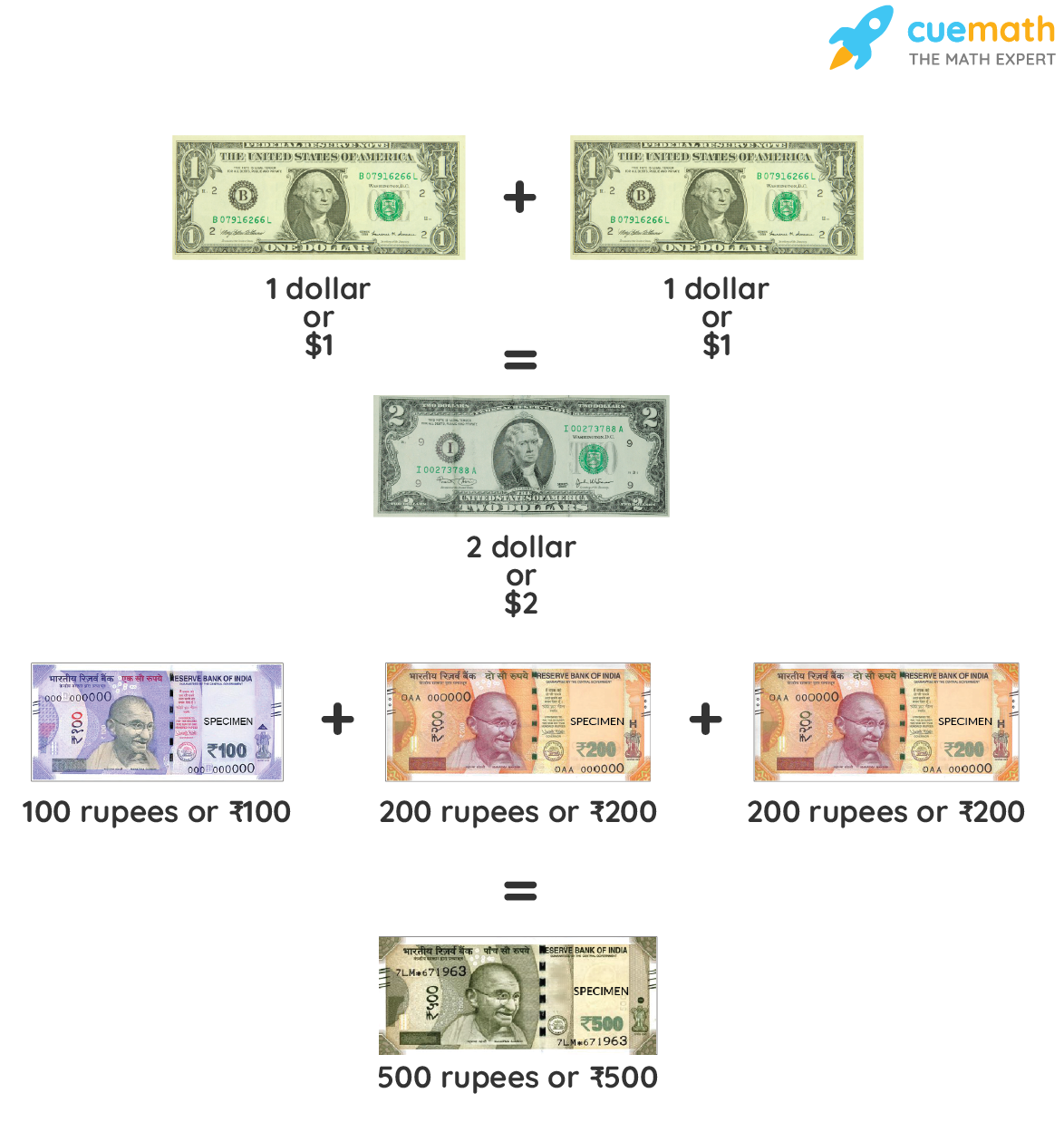
Money is what makes the world go round, and mathematics is the centripetal force that governs it. From simple transactions to banking, taxes, and discounts, everything that involves money, involves math! Money is a medium of exchange. We pay coins and notes in order to get services and commodities. You can now learn more about the process of identifying denominations and the concept of decomposing money.
All transactions are done using the country’s system of money i.e. currency. Money is something that we all interact with in some way on a daily basis and we end up falling back on our math skills to handle that money reliably.

A ratio tells us how much of the proportion of one thing to the other. The sequence (or order) in which the numbers in a ratio are written matters. The ratio is defined as the relation between the quantities of two or more objects and it indicates the amount of one object contained in the other. It is written in the form of a:b, where the first term, i.e 'a' is known as antecedent and the second term, i.e 'b' is known as consequent. Let's go ahead and learn about the concept of Ratios.
Example: 1 tablespoon of lemon concentrate+ 5 tablespoon of water = a perfect lemonade. The ratio to get a perfect lemonade can be expressed as Lemon Concentrate: Water = 1:5.
Example: 1:3 and 9:27 are equivalent ratios. They are in proportion. It is represented as 1:3::9:27. And is read as 1 is to 3 as 9 is to 27.
The percentage is defined as a given part or amount in every hundred. It is a fraction with 100 as the denominator and is represented by the symbol "%". The percentage is a fraction or a ratio in which the value of the whole is always 100. For example, if Sam scored 30% marks on his math test, it means that he scored 30 marks out of 100. It is written as 30/100 in the fraction form and 30:100 in terms of ratio. Percent means “out of 100”. If 20 out of 100 boxes are shaded, then we say that 20 percent or 20 of the boxes are shaded. You can now learn how to calculate Percentages and their applications with the help of examples.
Example: What is 30% of 750?
Solution: 30% of 750 = (30/100) × 750 = 225.
The unitary method, in essence, is all about finding the “per unit value”. The unitary method is a technique for solving a problem by first finding the value of a single unit, and then finding the necessary value by multiplying the single unit value. You can try solving some of the examples of the Unitary Method to understand the methods used in solving such problems.
Example: The cost of 4 lemons is $20. The cost of 1 lemon is 20/4 = $5. So, the cost of 10 lemons= 10 × 5 = $50.
Profit is the gain that is incurred when the Selling Price (SP) of a commodity is greater than its Cost Price (CP). Loss is incurred when the Selling Price (SP) of a commodity is less than its Cost Price (CP). Profit and Loss are the basic driving forces of the market, and here you will understand how to wield the power of mathematics and apply it to the commercial world.
Example:

Simple Interest is the interest that is calculated on the Principal Amount on a monthly, quarterly, or annual basis. Ever borrow money from a friend or relative and they said that you would have to return the amount after a year with 10% interest? The concept of Simple Interest will help you easily calculate the total amount you would need to repay them.
Example:

Compound Interest is the interest that is calculated on the Principal Amount and the Interest that is obtained from the previous term. Compound Interest is usually charged by banks and insurance companies on the amount of loan taken by us from them.
Example:

Discount is a reduction in the price of a commodity. It is the difference between the selling price and market price. Discounts are probably the most frequent terms that come up during a shopping trip or any purchase that we make since they directly affect the amount of money involved.
Example:

The government charges a fee on every item that is sold. This fee is meant to be spent on public welfare and is known as tax. The tax charged is always a percentage of the SP. You must have heard words like income tax, GST, service tax, etc in daily conversations. Let’s now try and understand how Taxes are levied on products.
Example: A packet of homemade chocolates costs $50. A service tax of 10% is charged. What will be the total bill amount?
Solution:
Service Tax= 50 × 10/100 = $5
The total bill amount including taxes= Cost price + Tax = $50 + $5 = $55.
Example 1: If Emma borrowed a sum of $40500 for a period of 21 months at 20% per annum, how much simple interest will she pay? Solution: The principal amount is $40500 and the rate of interest is 20% = 20/100. The time period given is 21 months = 21/12 years. Using the formula for interest I= P×R×T; I= 40500 × (20/100) × (21/12), so I= $14175. Therefore, Emma is going to pay $14175.
Example 2: David bought a new cell phone for $90. The value of the phone decreases by 3% on its original price every year. Find the value of his mobile after 3 years. Solution: 3% of 90 is: $2.7. The phone depreciates by $2.7 every year. Thus, the value of the mobile after 3 years will be: 90 - (3×2.7) = $81.9 Therefore, the value of the mobile after 3 years will be $81.9
Show Solution >
Math will no longer be a tough subject, especially when you understand the concepts through visualizations.